Réflexions : Pensées mathématique et informatique
Mathématiques et informatique : une histoire de famille[1]…
Entre pensée mathématique et pensée informatique.
L’informatique n’échappe pas à la dialectique outil-objet dans l’apprentissage des concepts[2]. En effet, depuis plusieurs années, l’enseignement des mathématiques utilise différents outils numériques que sont les logiciels de géométrie dynamique, les tableurs, les calculatrices et les logiciels de calcul formel. Aujourd’hui, la programmation a fait son entrée dans les programmes du cycle 4 et au lycée. L’algorithmique et la programmation semblent donc maintenant devenues des objets d’enseignement à part entière à travers les langages préconisés dans les documents ressources, à savoir Scratch et Python. Dans le supérieur, l’informatique constitue à la fois un outil dans l’apprentissage des mathématiques et reste un objet d’enseignement.
Les programmes du cycle 4 incitent à programmer principalement des jeux c’est-à-dire des situations concrètes d’images animées. Au lycée, la programmation doit être pratiquée autour des différents domaines des mathématiques (arithmétique, probabilités, géométrie, etc.) afin d’aider à l’apprentissage de concepts rencontrés dans des situations et des problèmes.
L’informatique et les mathématiques font appel à des formes de pensées. La pensée mathématique et la pensée informatique ne semblent pas a priori identiques.
Ce triptyque situation – pensée mathématique – pensée informatique s’articule autour de la modélisation mais aussi autour des choix didactiques lorsqu’on souhaite enseigner conjointement mathématique et informatique à travers une situation.
Ces pensées interagissent-elles ? S’enrichissent-elles mutuellement ? S’opposent-elles ? Quel rôle joue la situation dans cette interaction potentielle ?
A travers quatre exemples, on va s’intéresser à la place de la pensée mathématique et de la pensée informatique par rapport à la modélisation de la situation. On s’interrogera dans le même temps sur la manière dont ces deux pensées influencent les choix didactiques pour créer une activité dans le cadre d’un enseignement.
Les deux premières situations relèvent du domaine des mathématiques. Le troisième exemple aborde une situation concrète. Enfin le dernier exemple se situe dans le domaine informatique.
Arithmétique : la primalité d’un entier naturel.
Lorsqu’on se fixe comme problème de tester la primalité d’un entier naturel, on se place d’emblée suivant un point de vue mathématique : la définition d’un nombre premier s’impose. C’est un entier naturel supérieur ou égal à 2 qui n’admet que deux diviseurs (1 et lui-même) comme 17 ou 23. Ainsi un entier naturel supérieur ou égal à 2 n’est pas premier mais composé dès qu’il admet un diviseur autre que 1 et lui-même comme 35 qui est divisible par 5 ou 36 qui est divisible par 6 (un élève dirait que 36 est dans la table de 6).
En s’appuyant sur ces deux visions de la définition mathématique, rechercher si un nombre entier donné est premier ou composé peut consister à compter les diviseurs d’un entier donné (s’il en a uniquement deux, il est premier) ou bien à tester des entiers de plus en plus grands à partir de 2 jusqu’à en trouver un qui divise l’entier : cela se produit forcément avec l’entier donné (dans ce cas, il est premier). Mais en réalité, le mathématicien teste des entiers premiers à partir de 2 : si 2 ne divise pas l’entier en question, les autres entiers pairs sont évincés des tests suivants…
Si on se place du point de vue de l’informaticien, il ne va pas procéder de ces façons mathématiques : compter les diviseurs d’un entier qui peut être grand s’avère long en balayant tous les entiers de 1 à ce nombre. Pensez à un entier tel que 123 456 791 qui est premier ! De même, il est difficile de tester uniquement des entiers premiers pour déterminer si ce sont des diviseurs : il faudrait avoir recours à une liste de nombres premiers a priori inférieurs à l’entier testé… pour savoir s’il est lui-même premier ! L’informaticien ne voit donc pas les choses du même point de vue que le mathématicien. En effet, il lui parait plus efficace d’envisager de tester des entiers à partir de 2 jusqu’à obtenir un diviseur : une boucle conditionnelle convient parfaitement à cette tâche et elle s’arrêtera au pire obligatoirement sur l’entier lui-même s’il est premier.
Dans tous les cas, la boucle se termine sur la détermination d’un diviseur qui est premier.
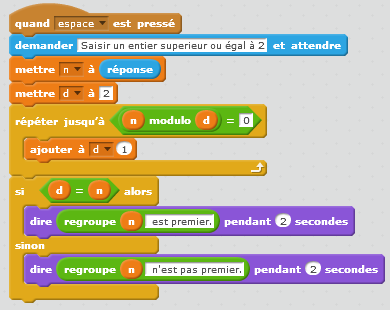
Ce programme permet de trouver le premier diviseur, supérieur ou égal à 2, du nombre testé.
Si ce diviseur est le nombre lui-même, c’est qu’il est premier.
On peut noter que ce programme fournit une réponse correcte pour 0 mais ne se termine pas pour 1 (la boucle ne s’arrête pas).
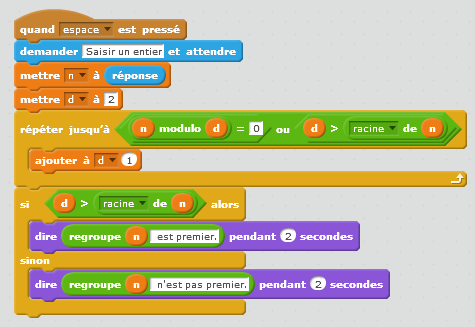
On perçoit ici deux choses à propos des pensées mathématique et informatique.
La première pointe des modes de résolution de problèmes assez différents : le mathématicien s’attache davantage à des stratégies qui s’appuient sur les objets mathématiques utilisés et sur leurs propriétés (ici les entiers naturels et leurs diviseurs) alors que l’informaticien recherche une stratégie efficace en temps voire en espace pour réaliser la tâche.
Le second élément est que chacune de ces deux pensées se nourrit de l’autre : l’informaticien améliore son algorithme grâce à des propriétés mathématiques sur les entiers naturels mais le mathématicien se servira de cet algorithme pour identifier des nombres premiers assez grands, une tâche difficile à la main, même avec une calculatrice.
Si on se place maintenant dans une activité pour la classe, on peut choisir de donner la définition d’un nombre premier et on peut demander d’écrire un algorithme ou un programme dans un langage donné qui teste la primalité d’un entier donné. L’élève ou l’étudiant est confronté à des choix de stratégies qui s’appuient principalement sur cette définition : il aura de grandes difficultés à s’en détacher pour envisager des stratégies qui relèvent plus de la pensée informatique…
Lors d’une séance de formation sur Scratch, des enseignants de mathématiques ont proposé les programmes suivants pour tester la primalité d’un entier :
Ces programmes comptent le nombre de diviseurs (avec ou sans liste). On peut noter qu’ils fournissent également la réponse attendue avec 0 et 1. Cependant, pour 0, la justification mathématique (infinité de diviseurs) s’oppose à la valeur du compteur ou à la longueur de la liste qui est nulle dans les deux cas.
On pourrait construire une activité à partir d’un programme dans le but de faire découvrir une définition d’un nombre premier : ce programme ne risque-t-il pas de privilégier une stratégie qui ne serait pas en lien direct avec la définition recherchée à moins de fournir un programme que l’informaticien ne mettrait pas en œuvre (une boucle itérative qui compte les diviseurs d’un entier donné) ... On voit bien ici aussi que pensée mathématique et pensée informatique ne vont pas forcément de pair pour enseigner l’une ou l’autre : la prégnance de l’une peut gêner l’émergence de l’autre.
On peut imaginer cependant proposer un tel programme avec une boucle itérative pour amener cette propriété sur les entiers naturels et définir les nombres premiers pour ensuite demander de modifier ce programme afin de le rendre plus efficace en temps… Un choix didactique en quelque sorte qui favorise un aller-retour entre les pensées mathématique et informatique.
Arithmétique : décomposition en produit de facteurs premiers d’un entier naturel.
La tâche qui consiste à déterminer la décomposition en produit de facteurs premiers d’un entier naturel supérieur ou égal à 2 fait appel à des stratégies mathématiques variées : la première consiste à décomposer l’entier en un produit de deux entiers plus petits, différents de 1, puis de recommencer jusqu’à ce que ce ne soit plus réalisable. Ainsi 24 s’écrit 4 x 6 et comme 4 s’écrit 2 x 2 et 6 s’écrit 2 x 3 alors 24 s’écrit 2 x 2 x 2 x 3 qui ne peut plus se décomposer… Cette stratégie fonctionne bien pour des nombres assez petits (car les nombres premiers utilisés sont eux aussi petits).
Une autre stratégie consiste à rechercher le plus petit diviseur premier de l’entier à décomposer, puis à effectuer la division et à recommencer avec le quotient obtenu jusqu’à parvenir à 1. Les facteurs premiers obtenus à la suite sont égaux ou de plus en plus grands. Cette stratégie fonctionne parfaitement pour tous les entiers mais elle peut être ardue s’il faut trouver des diviseurs premiers grands.
Elle est perfectible en utilisant le fait que ce plus petit diviseur premier est inférieur ou égal à la racine carrée de l’entier ciblé et cela après chaque division par un tel diviseur premier. Il n’est alors plus nécessaire de diviser afin d’obtenir 1 parce que le dernier quotient différent de 1 qui reste est alors premier de fait (c’est le dernier facteur premier).
Par exemple, lorsqu’on décompose 3 456 712, on trouve 2 comme plus petit diviseur premier de 3 456 712 et 1 728 356 comme quotient puis on trouve à nouveau 2 comme plus petit diviseur premier de 1 728 356 et 864 178 comme quotient puis on trouve encore 2 et le quotient est alors 432 089 (dont la racine carrée est autour de 657). 432 089 n’est pas divisible par 3 ni par 5 mais est divisible par 7 et le quotient vaut 61 727 (dont la racine carrée est autour de 248). 61 727 n’est pas divisible par 11, ni par 13 mais par 17 et le quotient est égal à 3 631 (dont la racine carrée est autour de 60). Comme 3 631 n’est pas divisible par 19, ni par 23, ni par 29, ni par 31, ni par 37, ni par 41, ni par 43, ni par 47, ni par 53 ni par 59 (10 tests sont nécessaires) alors il est premier et il constitue le dernier facteur de la décomposition qui s’écrit 2 x 2 x 2 x 7 x 17 x 3 631. La valeur du plus grand diviseur premier utilisé n’a pas atteint 100 pour un entier initial qui dépasse les trois millions.
Si l’on veut programmer cette tâche, on peut avoir recours à une liste ordonnée de nombres premiers mais sa création prend du temps tout comme son utilisation. Le programme est plus rapide à nouveau si on s’affranchit des diviseurs premiers en prenant des entiers successifs pour diviseurs comme pour le test de primalité. La boucle conditionnelle comprend une seule condition, soit l’égalité de l’entier n à 1, soit le fait que le diviseur d doit être inférieur ou égal à la racine carrée de n suivant la stratégie employée.
Les pensées mathématique et informatique semblent plus proches ici si on fait abstraction des diviseurs premiers. Cette proximité favorise l’accès à une technique de décomposition à partir de l’étude de l’exécution d’un programme utilisant une boucle conditionnelle avec le test de la condition sur l’égalité de l’entier n à 1. Cela constitue un choix didactique intéressant au collège pour introduire cette notion d’arithmétique. L’utilisation de l’autre condition sur le diviseur améliore le programme précédent en s’appuyant sur un résultat mathématique mais en masquant davantage la méthode de décomposition : on retrouve ici le fait que les deux pensées sont duales mais que l’une et l’autre peuvent constituer un obstacle à l’apprentissage visé.
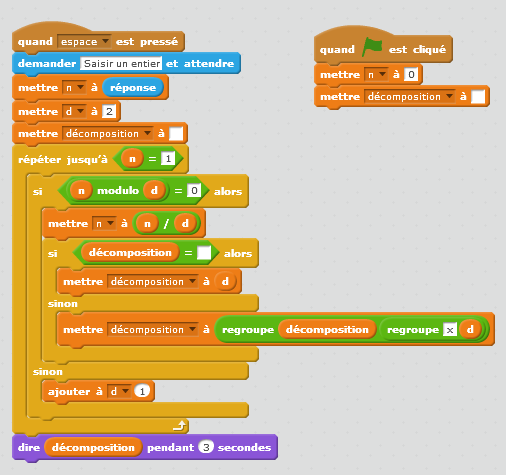
Une activité possible en classe consiste à proposer le programme suivant et demander aux élèves de l’exécuter à la main avec des entiers simples comme 44, 60 ou 74. Les élèves prennent conscience assez rapidement que certains tests sont inutiles au vu des tests déjà réalisés durant la décomposition.
On peut ainsi conduire les élèves à ne tester que les entiers premiers comme diviseurs. Emerge ainsi un algorithme mathématique de décomposition en produit de facteurs premiers.
On pourra ensuite améliorer cet algorithme en limitant les tests aux diviseurs premiers inférieurs ou égaux à la racine carrée du dernier quotient obtenu et écrire un programme plus performant.
Probabilité : la roue tourne.
On s’intéresse ici à la situation d’une roue qui tourne : elle est munie d’un index fixe (flèche noire) qui détermine un secteur de couleur lorsque la roue s’arrête. Cette roue est partagée en douze secteurs de couleurs de même taille : un bleu, deux verts, quatre rouges et cinq jaunes.
Contrairement aux deux exemples précédents qui s’appuient sur des tâches intra mathématiques, la situation est extra mathématique et demande d’être analysée préalablement pour pouvoir ensuite la modéliser mathématiquement et informatiquement : elle a donc une influence sur les pensées mathématique et informatique.
Si on regarde la situation réelle, faire tourner la roue manuellement nécessite d’y mettre une certaine force et les frottements réduisent sa vitesse peu à peu jusqu’à son arrêt complet : chaque secteur de couleur est-il alors équiprobable ?
La modélisation informatique peut se faire avec Scratch, langage de programmation qui produit des images dynamiques. Le programme doit permettre l’animation de cette roue et la production de simulations dans le cadre des programmes du cycle 4. Trois tâches sont donc à réaliser : faire tourner la roue, la faire s’arrêter au hasard (nous reviendrons plus loin sur ce point) et relever la couleur obtenue. Deux lutins sont nécessaires : une roue mobile et un index (flèche) fixe. Différentes stratégies sont possibles mais des instructions de mouvement, le générateur de nombres aléatoires et les capteurs de couleurs sont indispensables. Une bonne connaissance du langage s’impose. La charge informatique importante et la prégnance de la situation réelle font obstacle à la pensée mathématique qui leur correspond.
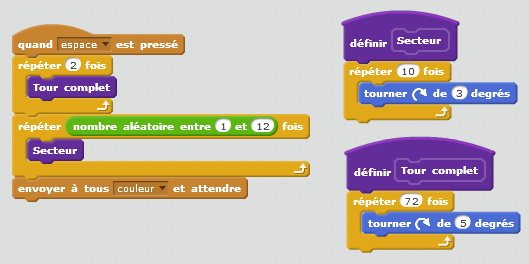
Voici un exemple de programmation proposé par des enseignants de mathématiques en formation continue qui répond aux trois tâches précédemment évoquées :
Ces scripts fonctionnent et répondent à la situation proposée.
Sont-ils cohérents avec l’analyse mathématique du problème ? De ce point de vue, chacun des secteurs de la roue doit être équiprobable. Ici huit secteurs ont une probabilité égale à 1/8 tandis que les quatre autres ont une probabilité nulle. Pourtant, en relançant le programme un grand nombre de fois, on constate que la fréquence d’apparition de chaque secteur de la roue se rapproche de 1/12.
Ce phénomène troublant s’explique du fait que chaque nouvelle exécution du programme n’a pas le même secteur de départ et ne représente donc pas une expérience identique à la précédente : par exemple, le secteur unique bleu peut n’avoir aucune chance d’apparaitre ou bien une chance sur huit suivant où est située la flèche qui indique le secteur de départ. Ici la loi des Grands Nombres ne s’applique pas de fait : il s’agit de la convergence d’une chaîne de Markov vers un état stable. On ne se situe pas dans une approche fréquentiste d’estimation d’une probabilité d’obtenir un secteur donné pour une seule et même expérience mais dans l’estimation de la probabilité d’obtenir un secteur donné après n étapes successives, n étant un entier de plus en plus grand. Ces connaissances mathématiques disqualifient ce programme qui fonctionne pourtant d’un point de vue informatique. Il convient de le corriger en utilisant l’opérateur « nombre aléatoire entre 1 et 12 » qui correspond aux douze secteurs de la roue et assure leur équiprobabilité mais on peut également choisir tout intervalle d’entiers contenant douze, ou un multiple de douze, valeurs consécutives. Ainsi le choix d’un nombre aléatoire entre 1 et 12, 1 et 24, 1 et 36 … s’impose naturellement. On peut cependant envisager un intervalle d’entiers consécutifs entre 13 et 24, 13 et 36 ou 25 et 36 … qui permet de faire tourner la roue obligatoirement de 1 ou 2 tours complets avant son arrêt aléatoire : ces intervalles permettent ainsi d’obtenir une image visuelle dynamique qui se rapproche davantage encore de notre perception de la rotation de la roue de loterie. Choisir l’opérateur « nombre aléatoire entre 28 et 39 » permet également d’obtenir une simulation cohérente avec le modèle mathématique d’équiprobabilité des secteurs mais ne constitue pas un choix didactique pertinent. Il n’est alors pas nécessaire de réinitialiser la position de la roue parce que l’équiprobabilité des secteurs est respectée. En effet, on peut faire tourner la roue au préalable pour qu’elle s’arrête sur un secteur déterminé aléatoirement à l’aide de l’opérateur « nombre aléatoire entre … et … » avec deux bornes quelconques, ce secteur fera office de secteur de départ.
Cette rotation aléatoire peut être effectuée avant ou après la phase de tirage au sort du secteur : les probabilités demeurent inchangées. On pourra lire en annexe des compléments sur ces points.
ffCes programmes permettent de se rapprocher de la situation réelle en faisant tourner la roue d’un certain nombre de secteurs suffisant qui peut dépasser un tour complet. Est-ce un programme pertinent à proposer aux élèves du cycle 4 ? D’autres choix didactiques semblent s’imposer. Il faudrait mieux proposer des tours complets et éviter l’utilisation de deux tirages aléatoires.
Les tours complets permettent de ne pas interférer avec l’objectif visé à savoir travailler sur un tirage aléatoire entre 1 et 12 qui relève de l’équiprobabilité des secteurs et correspond à l’arrêt au hasard de la roue.
Ce choix de nombre aléatoire entre 1 et 12 demeure plus aisé à gérer par l’élève qu’un intervalle d’entiers d’extrémités1 et 24, 1 et 36 … car il lui permet d’associer à chaque secteur coloré un seul nombre entier.
De plus, si un objectif de l’activité consiste à aborder les probabilités à travers une approche fréquentiste, il faut renouveler la même expérience aléatoire un grand nombre de fois. Un des paramètres importants est la position de la roue au départ du lancer : il faut donc réinitialiser sa position initiale sur le même secteur, à chaque déclenchement du programme, afin d’éliminer cet élément variable qui, malgré tout, comme nous l’avons démontré précédemment, n’a aucune influence, ni sur la probabilité de chaque événement (couleur obtenue), ni sur la convergence des fréquences.
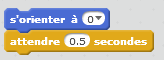L’ajout des ces deux instructions en début de programme suffit pour répondre à cette exigence :
Une activité élève pourrait alors consister à compléter certains éléments du script ci-dessus.
On peut noter que l’opérateur « nombre aléatoire entre … et … » génère des entiers pseudo-aléatoires : pour diminuer les biais induits par cette méthode, les développeurs en informatique utilisent souvent un intervalle d’entiers plus grand associé à la fonction modulo 12 (en ajoutant 1) pour obtenir des entiers aléatoires « mieux » uniformément répartis entre 1 et 12.
Dans cette situation de la roue, l’image dynamique est prégnante. Elle occupe le premier plan dans la programmation informatique au détriment de la pensée mathématique et des lois de probabilités associées. La maîtrise du langage informatique est la condition indispensable pour atténuer cet obstacle. Après avoir surmonté ces difficultés, l’enseignant devra veiller à faire des choix pertinents pour créer une activité faisant émerger les notions mathématiques visées (probabilité, approche fréquentiste, angles et rotation, …).
De Scratch à Python : une transition douce !
Prenons maintenant comme exemple un programme de primalité proposé précédemment : la situation consiste à le traduire dans le langage Python. Il s’agit ici d’une situation intra informatique a priori.
Une personne maitrisant suffisamment les deux langages pourrait envisager une traduction de briques ou groupes de briques Scratch en instructions textuelles Python. Cette traduction pourrait se faire quasi automatiquement sans nécessiter de prise de sens à condition de posséder une certaine aisance technique.
Un novice dans le langage Python doit au préalable passer par une analyse reposant sur l’algorithme sous-jacent du programme. Il doit identifier alors les phases d’initialisation/entrée, traitement et sortie qui structurent l’algorithme. Un élève de seconde devrait donc s’être familiarisé à ce travail algorithmique au cycle 4.
Les briques « demander… » et « mettre n à réponse » correspondent à une action de saisie en algorithmique (Saisir n, Lire n, Entrer n, …) qui se traduit par une instruction textuelle unique en Python « n=int(input("saisir un entier")) ». Le décalage entre l’écriture avec des briques de Scratch et celle en Python nécessite une analyse algorithmique pour donner du sens.
L’instruction « mettre d à 2 » pourrait se situer dans la partie « traitement ». La variable d doit être créée sous Scratch puis initialisée tandis que sous Python, ces deux étapes sont simultanées lors de l’écriture de l’instruction « d = 2 » ; on peut remarquer l’affectation en Python à l’aide du signe =, écriture ici non symétrique contrairement à l’égalité mathématique.
En sortie, l’affichage conditionnel sous Scratch est assez proche de celui en Python :
On peut noter que la concaténation de n et du texte « est premier » n’est pas nécessaire sous Python : les deux éléments s’affichent à la suite l’un de l’autre. D’autre part, afin d’éviter d’importer une bibliothèque sous Python, on peut remplacer d> racine(n) par d²>n ce qui nécessite une traduction mathématique de la condition.
Dans la phase de traitement, on utilise une boucle conditionnelle introduite sous Scratch par la brique « répéter jusqu’à … ». Cette instruction correspond en algorithmique à la boucle « Tant que » traduite par « while » dans de nombreux langages dont Python.
En première analyse, la boucle « Tant que » en algorithmique est suivie d’un prédicat tandis que les instructions « répéter jusqu’à » sous Scratch et « while » sous Python sont suivies d’une proposition : en effet, dans un programme, les variables sont affectées et la condition devient une proposition possédant une unique valeur de vérité (instanciation). Le « Tant que » en algorithmique se traduit littéralement par « while » sous Python : la boucle s’arrête lorsque la proposition est fausse. Sous Scratch, la boucle se termine lorsque la proposition est vraie. Lors de l’exécution, il y a comparaison de la valeur de vérité de la proposition avec la valeur « vrai ». La proposition du « while » doit donc être la négation de la proposition du « répéter jusqu’à » pour une même condition. C’est ici que la pensée mathématique intervient pour assurer la traduction de la condition d’un langage à l’autre à l’aide de la logique mathématique. Plusieurs stratégies sont possibles : la plus simple consiste à traduire « répéter jusqu’à P », P étant une proposition, par « while P == False », « P == False » étant une nouvelle proposition qui peut être vraie ou fausse.
Une autre solution peut consister à nier la proposition utilisée sous Scratch à l’aide de l’opérateur booléen « not ».
Une stratégie différente qui s’appuie sur un travail de logique en mathématique permet d’arriver à une autre écriture, pas nécessairement plus simple mais plus souvent utilisée :
La formulation des propositions est davantage affirmative que négative ; on ne rencontre que très rarement la condition :
Tout ceci permet de rencontrer en mathématique différents éléments de logique : proposition, valeur de vérité, négation d’une proposition, connecteurs logiques et leurs propriétés.
Une analyse plus fine montre cependant que la pensée informatique diffère de la pensée mathématique.
En effet, d’un point de vue mathématique, une condition est perçue comme un prédicat dont on étudie les valeurs de vérité successives (vrai ou faux) des propositions lors de l’exécution du programme : on effectue la boucle conditionnelle tant que la valeur de vérité de la proposition est vraie.
D’un point de vue informatique ou plutôt machine, la condition est assimilée à une valeur qui est comparée à 0 et non à « vrai » : tant que cette valeur est différente de 0, les instructions de la boucle sont effectuées. Ainsi le programme suivant ne s’arrête pas et affiche les entiers successifs à partir de l’entier saisi.
"valise" est une chaine de caractères qui n’est pas égale à 0… ni à 1. Ce n’est pas non plus une proposition. Mais la machine exécute tout de même les instructions.
En mathématiques, ce qui n’est pas faux est vrai. En informatique, ce n’est pas toujours le cas : il semble qu’on puisse écrire des conditions qui ne soient pas des propositions sans obtenir un message d’erreur. On peut aussi proposer des écritures qui semblent être la négation l’une de l’autre d’un point de vue mathématique et qui soient toutes les deux fausses d’un point de vue informatique (pas de message d’erreur et affichage de False) :
L’opérateur booléen « not » de Python ne fournit pas la négation de la proposition mais transforme la valeur de vérité de 0 en 1 ou inversement.
Un élève pourrait commettre assez facilement des erreurs d’écriture comme celles qui suivent :
Ces écritures n’empêchent pas l’exécution du programme, la première produit une boucle infinie, la seconde ne permet pas d’exécuter les instructions de la boucle. Ainsi cette instruction placée dans le programme de primalité produit les résultats suivants sur les nombres testés 15, 11 et 3.
Seuls les nombres 2 et 3 sont reconnus comme nombres premiers mais pour de mauvaises raisons…
L’analyse de cette situation montre que la traduction d’un programme écrit sous Scratch en Python n’est pas automatique pour un élève découvrant ce nouveau langage. Il doit faire appel à ses connaissances mathématiques, en particulier de logique, pour être capable de transcrire une boucle conditionnelle utilisant l’instruction « répéter jusqu’à … » en un « while … ». Les mathématiques viennent ici au secours de l’apprenti informaticien bien que la logique bivalente (vrai/faux) mathématique ne soit pas celle du langage machine (différent de zéro/égal à zéro). Les différences de fonctionnement entre variable mathématique et variable informatique augmentent les difficultés de traduction d’une condition pour passer d’un point de vue mathématique à la programmation. Quant à la situation proposée ici et au programme choisi, la double condition utilisée dans la boucle ne favorise pas cette transition douce de Scratch à Python. Il faudra bien évidemment initier les élèves à travers des programmes contenant des boucles élémentaires du type :
Conclusion:
Pour élaborer un algorithme et écrire un programme, l’élève doit bien souvent disposer de connaissances mathématiques bien installées, et ceci d’autant plus que la situation-problème proposée fait appel à un modèle mathématique élaboré. Le programme peut également, en retour, enrichir la pensée mathématique de l’apprenant. Les pensées mathématique et informatique se nourrissent donc l’une de l’autre mais ont cependant leur propre mode de fonctionnement (syntaxique, sémantique) et peuvent, dans certains cas, s’opposer. Dans le premier exemple, la puissance de calcul de la machine conduit à concevoir un programme de test de primalité qui, lors de son exécution, effectue des calculs jugés inutiles en mathématique. La complexité informatique n’est pas de même nature que la complexité mathématique : l’informaticien s’attache à une facilité de programmation, à une économie d’espace mémoire et à une rapidité d’exécution du programme tandis que le mathématicien recherche une démonstration la plus efficace en minimisant les calculs et les éléments d’argumentation utilisés. Nous trouvons également des différences dans l’emploi des variables et des fonctions (ou blocs sous Scratch) en informatique par rapport à leurs utilisations en mathématiques. Tout ceci montre que la pensée informatique diffère de la pensée mathématique et ces différences doivent être pointées par l’enseignant dans le cadre de l’apprentissage de la programmation.
Au lycée, les programmes incitent clairement à privilégier l’aspect outil de l’informatique au service des mathématiques sur l’aspect objet d’enseignement. Cependant, ils insistent sur la nécessité de travailler avec attention les notions de variable et fonction informatiques. La transition de Scratch à Python nécessite de surcroît un travail conséquent pour passer d’un langage pré-écrit à un langage textuel qui s’appuie sur l’algorithmique et la logique mathématique. En cela, l’informatique peut être perçue comme objet d’enseignement.
Les situations proposées et les variables didactiques associées devraient être choisies pour favoriser l’enrichissement mutuel de ces deux formes de pensée : l’aspect pédagogique en mathématiques peut conduire donc à proposer des programmes qui ne soient pas les plus pertinents pour l’informaticien.
Dans le secondaire, l’enseignement des mathématiques et de l’informatique doit permettre à ces deux modes de pensées de s’accompagner et de cohabiter en conservant leur fonctionnement propre.
Mis à jour le 31/08/2019
[1] Voir aussi l’article « Le logiciel Scratch au collège : un mariage de raison entre mathématiques et informatique », Repères IREM n° 110 de janvier 2018.
[2] Jeu de cadres et dialectique outil-objet dans l’enseignement des mathématiques de Régine Douady.